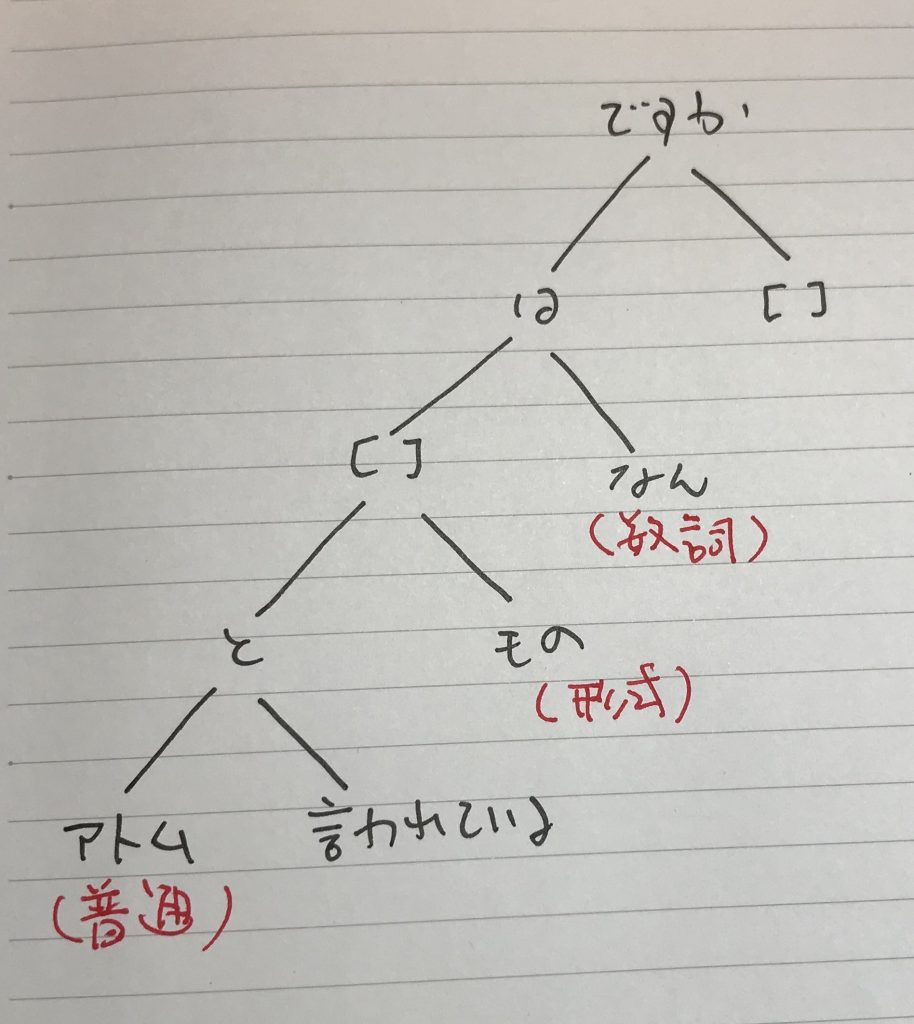
書き忘れていたが、この間、以前も使っていた二分木を平文にするプログラムを少し改良している。AIサーバー、AIクライアントで使っているので掲載しておく。
%%
%% prologツリーをベタな文章に変換して表示する
%% 全て、変数に出力されるように改訂
%%
wsprint(Sent,Out) :-
nb_setval(console,''),
printnode(Sent),
nb_getval(console,Out).
%% write(Out),nl.
%% グローバル変数 console に出力をつなげていく
wsappend(S) :-
nb_getval(console,Tmp),
atom_concat(Tmp,S,Out),
nb_setval(console,Out).
%% -----------------------
%%% 出力のclauses
%% -----------------------
% 対象がatomならば、そのまま表示
printnode(N) :- atom(N),wsappend(N).
%% 対象が空でないリストならば、最初の項の表示
printnode(N) :- [_|_] = N,showlist(N).
%% 対象が空リストならば'/'(半角スラッシュの表示)
%% printnode(N) :- [] = N,wsappend('/'). %% 空リストでもtrueにする
%% スラッシュやめる
printnode([]).
%% 対象が項ならば、元の言葉の順序で表示(語がnodeならば再帰的に表示する
%% ただし、node語がnodeは含まない)
printnode(N) :- node(X,Y,Z) = N,
printnode(Y),
printnode(X),
printnode(Z).
%% -----------------------
%% getlistは、リストが[語, カテゴリ]から構成されているのから、語だけのリストを作る
%% 一つのフレーズに複数の語があると
%% [[[語, カテゴリ],語],[語, カテゴリ]] などのように繋がってリスト化される
%% knpがカテゴリを出力しない場合は、語が単独になることもある
%% HeadとTailをから、それぞれの語を取り出して、結合したのを出力
%% -----------------------
getlist([H|[T]],[X1, X2]) :- getlist(H,X1),
getlist(T,X2),!.
%% 構造的に、Tailには、単位リストしか入っていない
getlist([H|[T]],[H,H1]) :- atom(H),[H1|_] = T,!.
%% tailがリストでない場合は、atomであるHeadのチェック
getlist([H|[_]],H) :- atom(H).
%% tailが構造化されたリストの場合にはここで処理する
getlist([H|[T]],[Z,T]) :- atom(T),
getlist(H,Z).
%% -----------------------
%% ベタなリストに変換するのがprintlist
%% swi-prologにflattenという組み込み関数がある
%% -----------------------
printlist(L) :- atom(L),
wsappend(L).
%% ベタなリスト化は、以下のclauseで単純に作れる
printlist(L) :- [H|[T]] = L,
printlist(H),
printlist(T),!.
%% -----------------------
%% getlistとprintlistを繋げるのがshowlist
%% -----------------------
showlist(L) :- getlist(L,X),
printlist(X).
実行例を示しておく。prolog二分木化したwikipediaからとってきているかなり複雑な二分木がだ、綺麗に日本語の平文に直している。
?- ['../lib/wsprint.swi']. true.
?- wsprint(node(は,[['デビュー', 'S:サ/C:抽象物/D:メディア'], 前],node(で,[[紫苑, 'S:普/C:植物'], [名義, 'S:普/C:抽象物']],node(と,[[杏樹, 'S:人'], [紫苑, 'S:普/C:植物']],node([],[いう, 'V:いう'],node(で,[コ ンビ, 'S:普/C:組織・団体'],node(の,[[耽美, 'S:普/C:抽象物'], [系, 'S:普/C:抽象物']],node([],[漫画, 'S:普/C:人工物-その他;抽象物/D:文化・芸術'],node(を,node(の,[],[パロディ, 'S:普']),node([],[[描いて, 'V:描く'], おり],node([],[[要, 'S:普/C:人工物-その他;抽象物'], [出典, 'S:普/C:抽象物/D:文化・芸術']],node(の,[[ 江口, 'S:人'], [寿史, 'S:人']],node([],[単行本, 'S:普/C:人工物-その他;抽象物/D:文化・芸術'],node(の,[[江口, 'S:地'], [寿史, 'S:人']],node(で,なんとかなる,node([],[ショ, 'S:サ'],node(の,[[江口, 'S:地'], [寿史, 'S:人']],node(に,[[[爆発, 'S:サ/C:抽象物'], ['ディナー', 'S:普/C:人工物-食べ物/D:料理・食事']], ['ショ ー', 'S:普/C:抽象物/D:文化・芸術']],node([],[[[[収録, 'S:サ/C:抽象物/D:文化・芸術;メディア'], [さ, 'V:する']], れて], いる],[ ])))))))))))))))))),Out).
Out = デビュー前は紫苑名義で杏樹紫苑というコンビで耽美系の漫画のパロディを描いており要出典江口寿史の単行本江口寿史のなんとかなるでショ江口寿史の爆発ディナーショーに収録されている .