表題のことがテーマである。
ずっと悩んでいる(笑)
(1)まず、片足に重心がほぼ乗っているかどうかの場合を分ける。
(2)乗っていない場合。乗っていなくても、相対的に重心がかかっている足は確定できる。その相対的支持足には四つのポイントがある。
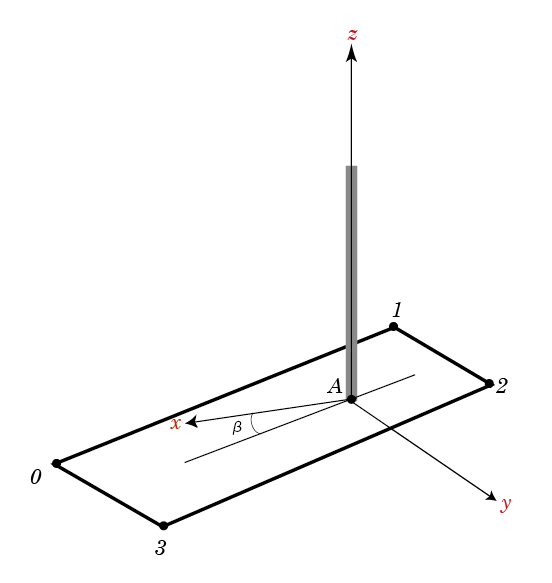 z軸の値が小さなものが少なくとも二つはあるはずだ。
z軸の値が小さなものが少なくとも二つはあるはずだ。
ロボットの体型が決まっていれば、その点を基準に他の足や脚の座標が全て決められるはずだ。
(※ここで注意しておくと、以後、足のくるぶしから先の部分を足(英語でfoot)といい、その他の英語でlegと言われる部分は脚ということにする)
その中で、z座標が負になるような点があったら、初めの2点の角度を変えて、それらの点がゼロになるように角度を変えなければならない。
逆に逆足が中空に上がってしまった場合は、そこを大地にくっつけるように回転させる必要がある。
(3)重心がその脚だけに乗っている場合は、その脚全体が大地についていることを前提に体型を載せる必要がある。そして、もし、逆足が大地から上がっている場合は、それをそのままにしておいて良い。重心がほとんど乗っていないわけだから。
月別: 2017年7月
シミュレータ、膝の動き
シミュレーターで、先のAshiro1のCosmファイルに膝を曲げる動きだけを加えたものを食わせて見た。
明らかに不自然だ。実際のロボットだったら変なことになっただろう。
シミュレーターがもっと自然な動きになるように工夫する必要がある。次の図を見てもらいたい。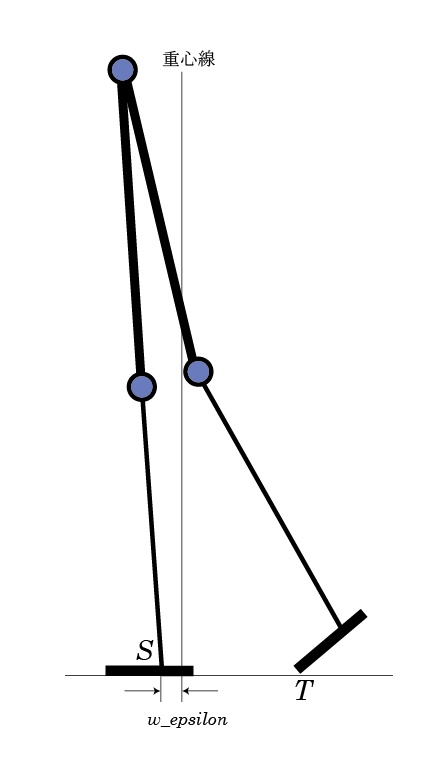
後ろになった足がかかとを曲げ高くすることによって膝が周り、体全体が前のめりになり、一体の状態まで来ると後ろ足が上がり、前足のみで立つようになる。
重心が支えている足の一定近くに来るまでは、後ろ足をあげられないようにすれば良い。
それまでは、T点とS点で支えるような形にするのである。
さらに、近傍の中に入って、反対側の足がつり上がっている状態においては、その足の足首の角度が体全体の傾きを規定する、とすれば良い。
また、この近傍の大きさは、体に働いている慣性力の影響を受ける。体が強く動いている時には、この近傍は大きくなるだろう。逆に、体がゆっくりとしか動いていないときは、相対的にこん近傍は小さくなる。
シミュレータの改良
重心を支えている足の位置を固定するようにした。先のものは、ロボットの原点を動かないようにしたので、形はサーボによる決まるものだが、不自然だった。
ただし、側面図では、前方へ歩いて行ってしまうし、正面図では、スクリプトが微妙に(こちら側に向いて)左側に開きが大きくしてあるものだから左側に動いて行ってしまう(笑)
足郎2のシミュレーターの第1段階、ほぼ出来上がる
この間、計算に次ぐ計算をやってきた、足郎2のシミュレーターだが、スクリプトからサーボを動かして、ロボットの形を作るところまでは、ほぼ出来上がった。このシミュレータに、COSMで書いたスクリプトを読み込ませて、動きを確認する程度には、実行させることができる。実際のロボットの動きにどれだけ近くなるかは、ロボットの方を組み上げてみないとわからないが、そちらは、業者に部品を作ってもらっているところなので、まず、シミュレータの動きを確認するしかない。
計算式が複雑なので、プログラムのバグを取るのに苦労した。
ただし、まだ、重心と着地した足の関係など、グローバルな座標で描いてはいない。ロボットの形をシミュレーションしているだけである。この動きを、重心との関係で、グローバルな座標に変換して表示するのはこれからの作業である。
このシミュレーターに足郎1を動かしたときのCOSMスクリプトを読み込ませて、動かしてみた結果が以下の動画である。
左が側面から見たもので、右側が正面から見たものであり、右足が緑色で、左足が青である。
足郎1には、膝がなかったので膝が動くスクリプトではないが、膝を動かすスクリプトも次に書いてみる。以下に、上記の動画の元になったスクリプトを記載しておく。
#######################################
# ashiro1-13.cosm
# 逆振り子二足歩行
# 2017年7月26日 作成
#######################################
%defspeed normal {
interval:3
steps:20
}
%defspeed fast {
interval:3
steps:10
}
#####################################
# かなり基本的なパラメータ
# いじるパラメータはここに置いておく
#####################################
# ただの逆振り子だと、40にすると倒れる
%param invpen_angle_right 35
%param invpen_angle_left 40
# 逆足を少し開いて、縮み加減にしないと倒れる
%param open_inv_right 15
%param open_inv_left 15
# 足を前に(わずかに)振り出す
%param step_forward 7
######################################
# 単純逆振り子
######################################
%defangles right_invpen {
#右に傾ける動きをする
RightUpperRight:-$invpen_angle_right+$open_inv_right
RightUpperLeft:+$invpen_angle_right-$open_inv_right
LeftUpperRight:-$invpen_angle_left
LeftUpperLeft:$invpen_angle_left
# 上の動きに合わせて、足も角度をつけて
RightLowerRight:$invpen_angle_right
RightLowerLeft:-$invpen_angle_right
LeftLowerRight:$invpen_angle_left
LeftLowerLeft:-$invpen_angle_left
}
%defangles left_invpen {
#左に傾ける動きをする
RightUpperRight:$invpen_angle_right
RightUpperLeft:-$invpen_angle_right
LeftUpperRight:$invpen_angle_left-$open_inv_left
LeftUpperLeft:-$invpen_angle_left+$open_inv_left
#
RightLowerRight:-$invpen_angle_right
RightLowerLeft:$invpen_angle_right
LeftLowerRight:-$invpen_angle_left
LeftLowerLeft:$invpen_angle_left
}
######################################
# 前へ
######################################
%defangles left_forward {
#左足を前に出す
RightUpperFront:-$step_forward
RightUpperBack:$step_forward
LeftUpperFront:$step_forward
LeftUpperBack:-$step_forward
}
%defangles right_forward {
#右足を前に出す
RightUpperFront:$step_forward
RightUpperBack:-$step_forward
LeftUpperFront:-$step_forward
LeftUpperBack:$step_forward
}
######################################
# 実行手続きの定義
# 即実行コマンドから最初に呼び出されるという意味で
# メインルーチン
# 初期歩行
######################################
%defexec walk {
#stand:all
exec:walk_sub,10
}
######################################
# サブルーチンの定義:通常歩行
######################################
%defexec walk_sub{
speed:normal
setAngle:right_invpen
speed:fast
setAngle:left_forward
speed:normal
setAngle:left_invpen
speed:fast
setAngle:right_forward
}
#################################
# 唯一の即実行プログラム:他は全て定義
# 全てはここから始まる
#################################
%exec walk 1
#################################
ロボット座標面への射影の長さの計算
ロボット座標の再構成(修正)
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_952661879ea9e8690c9083961fbdeeff.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_952661879ea9e8690c9083961fbdeeff.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_05e4f1cf37c12474111eb3fc0bbc54bb.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_05e4f1cf37c12474111eb3fc0bbc54bb.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_7869199cbdbbe885060095e7133873a1.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_7869199cbdbbe885060095e7133873a1.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_e49801ecf5f0c56fdb3cfa3d92dc021b.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_e49801ecf5f0c56fdb3cfa3d92dc021b.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_87ab620a1b65e290b01561a426cd7627.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_87ab620a1b65e290b01561a426cd7627.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_4f03003c68c9583501d3d1645e9ff6b5.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_4f03003c68c9583501d3d1645e9ff6b5.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_fdce3761401bf3575bb41968e827c82b.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_fdce3761401bf3575bb41968e827c82b.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_077c114cd766ed664afe08e26dfe6026.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_077c114cd766ed664afe08e26dfe6026.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_4bea4e4d3f5fbaeae04da51f3691e347.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_4bea4e4d3f5fbaeae04da51f3691e347.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2e470b9e996d73e580d67d836994de30.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2e470b9e996d73e580d67d836994de30.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_45878e175e6afe5f9d393ff3f55cee8d.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_45878e175e6afe5f9d393ff3f55cee8d.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
いざプログラムに書こうと思ったら、先の記事に書いた正面図が、ひざ関節が左右に曲がるというものになっているのに気づいた。足郎2は、ひざは前後にしか曲がらない(人間と同様)ので、修正した。
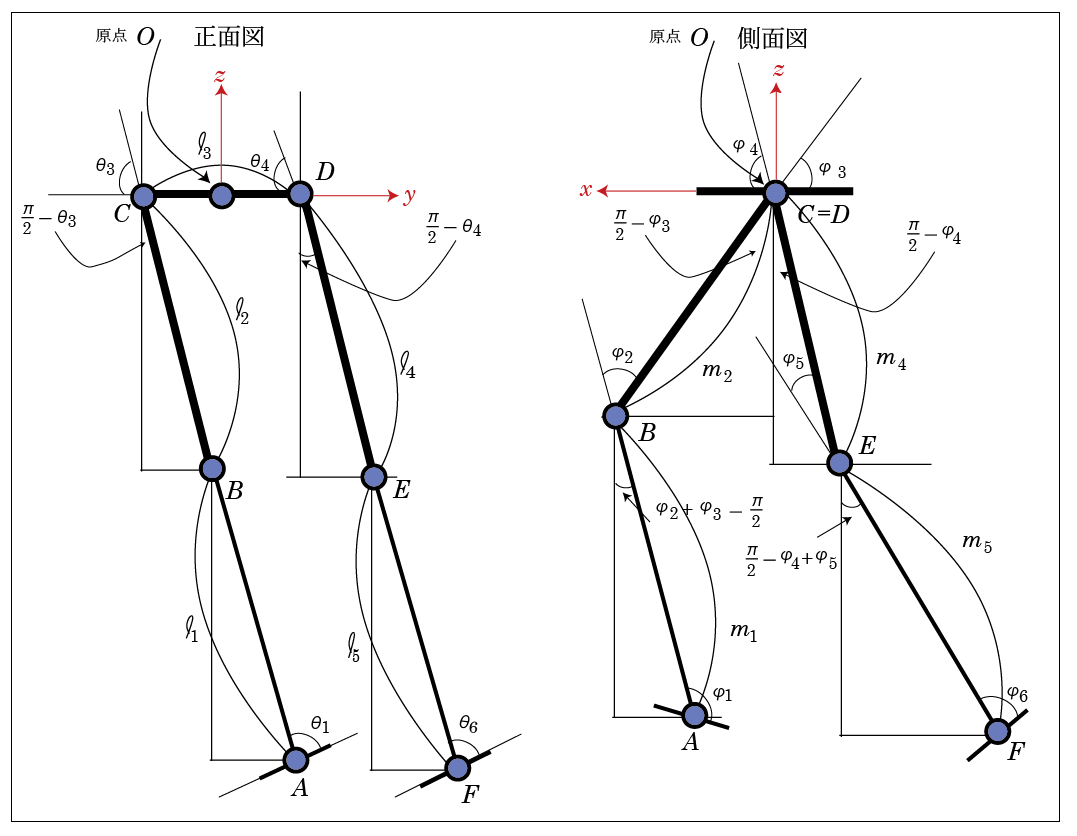
正面図は、変な格好だが、図は角度の正の向きを確認し、関節位置の座標を確定するためのものだから問題ない。
《正面図》
A点とB点の関係

B点とC点の関係

C点と原点の関係

D点と原点の関係

D点とE点の関係

E点とF点の関係

《側面図》
A点とB点の関係

B点とC点の関係

C点とD点と原点の関係

D点とE点の関係

E点とF点の関係

シミュレーションの長さの計算
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_d20caec3b48a1eef164cb4ca81ba2587.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_d20caec3b48a1eef164cb4ca81ba2587.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2db95e8e1a9267b7a1188556b2013b33.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2db95e8e1a9267b7a1188556b2013b33.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_6f8f57715090da2632453988d9a1501b.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_6f8f57715090da2632453988d9a1501b.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_e75f543693a864dd710a7fe5fbf2f18c.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_e75f543693a864dd710a7fe5fbf2f18c.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_6f8a8d586df38c4edd662446c8fe4e8c.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_6f8a8d586df38c4edd662446c8fe4e8c.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_767e055909f28f5d5f3dbec8cb996555.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_767e055909f28f5d5f3dbec8cb996555.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_d20caec3b48a1eef164cb4ca81ba2587.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_d20caec3b48a1eef164cb4ca81ba2587.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
一つ前の記事で、次に検討すると記述した長さについての関係性をまとめておく。
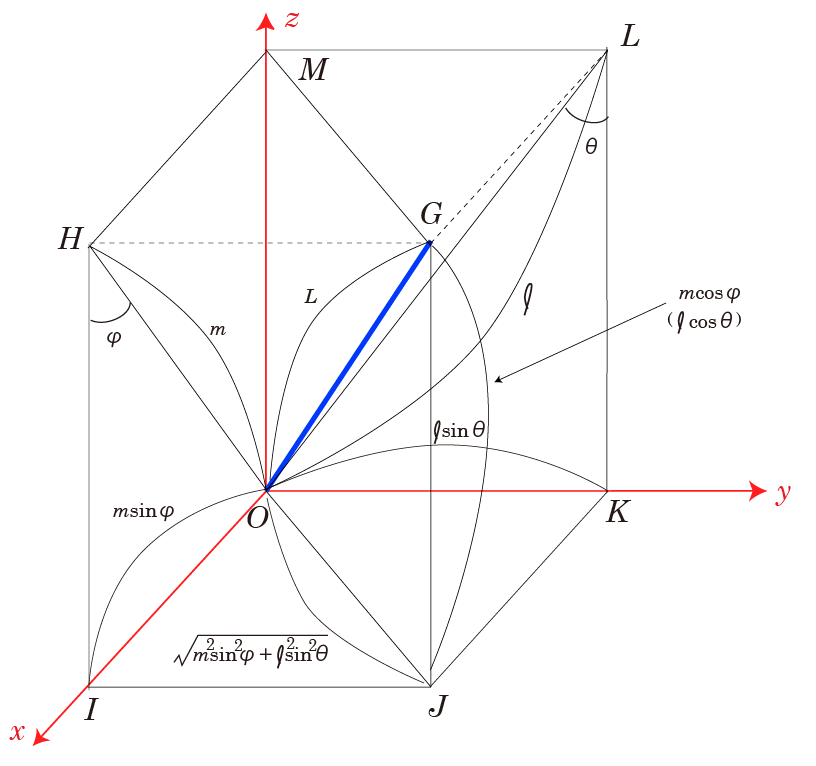
図において、OGは、足などの実体であり長さは である。この長さが正面図において見えているのが、OLである。また、側面図において見えているのがOHとなる、それらの長さは
である。この長さが正面図において見えているのが、OLである。また、側面図において見えているのがOHとなる、それらの長さは と
と である。正面図、側面図では、角度θとφが捉えられているとしよう。
である。正面図、側面図では、角度θとφが捉えられているとしよう。
このときまず、の位置は同じだから、

が成立する。
さらに、

が成立する。これら二つの式より、
 が
が と角度の値から求めることができる。
と角度の値から求めることができる。
ロボット座標の再構成
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_7e5d290f2c945d19c592c783c2f03074.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_7e5d290f2c945d19c592c783c2f03074.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_f348de7f2d9a074ea8f264b3bb25f791.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_f348de7f2d9a074ea8f264b3bb25f791.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_7a303b4dd027d975c12d916573764158.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_7a303b4dd027d975c12d916573764158.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_a8e656fc6473e86a99fd68fac55039b8.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_a8e656fc6473e86a99fd68fac55039b8.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_05e4f1cf37c12474111eb3fc0bbc54bb.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_05e4f1cf37c12474111eb3fc0bbc54bb.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_7869199cbdbbe885060095e7133873a1.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_7869199cbdbbe885060095e7133873a1.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_e49801ecf5f0c56fdb3cfa3d92dc021b.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_e49801ecf5f0c56fdb3cfa3d92dc021b.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_87ab620a1b65e290b01561a426cd7627.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_87ab620a1b65e290b01561a426cd7627.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_acc8061e6a3ae5a671b3556c17d71513.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_acc8061e6a3ae5a671b3556c17d71513.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_fdce3761401bf3575bb41968e827c82b.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_fdce3761401bf3575bb41968e827c82b.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_077c114cd766ed664afe08e26dfe6026.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_077c114cd766ed664afe08e26dfe6026.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_4bea4e4d3f5fbaeae04da51f3691e347.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_4bea4e4d3f5fbaeae04da51f3691e347.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2e470b9e996d73e580d67d836994de30.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2e470b9e996d73e580d67d836994de30.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_45878e175e6afe5f9d393ff3f55cee8d.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_45878e175e6afe5f9d393ff3f55cee8d.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_fbade9e36a3f36d3d676c1b808451dd7.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_fbade9e36a3f36d3d676c1b808451dd7.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2db95e8e1a9267b7a1188556b2013b33.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2db95e8e1a9267b7a1188556b2013b33.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_6f8f57715090da2632453988d9a1501b.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_6f8f57715090da2632453988d9a1501b.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_daca9878daaa869121f7dc2b8f751edd.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_daca9878daaa869121f7dc2b8f751edd.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_33bf7cf150b79380de8e13646d9e15af.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_33bf7cf150b79380de8e13646d9e15af.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
先の記事に書いて、シミュレーションで暫定的に動かしてみた座標の設定には、問題があった。
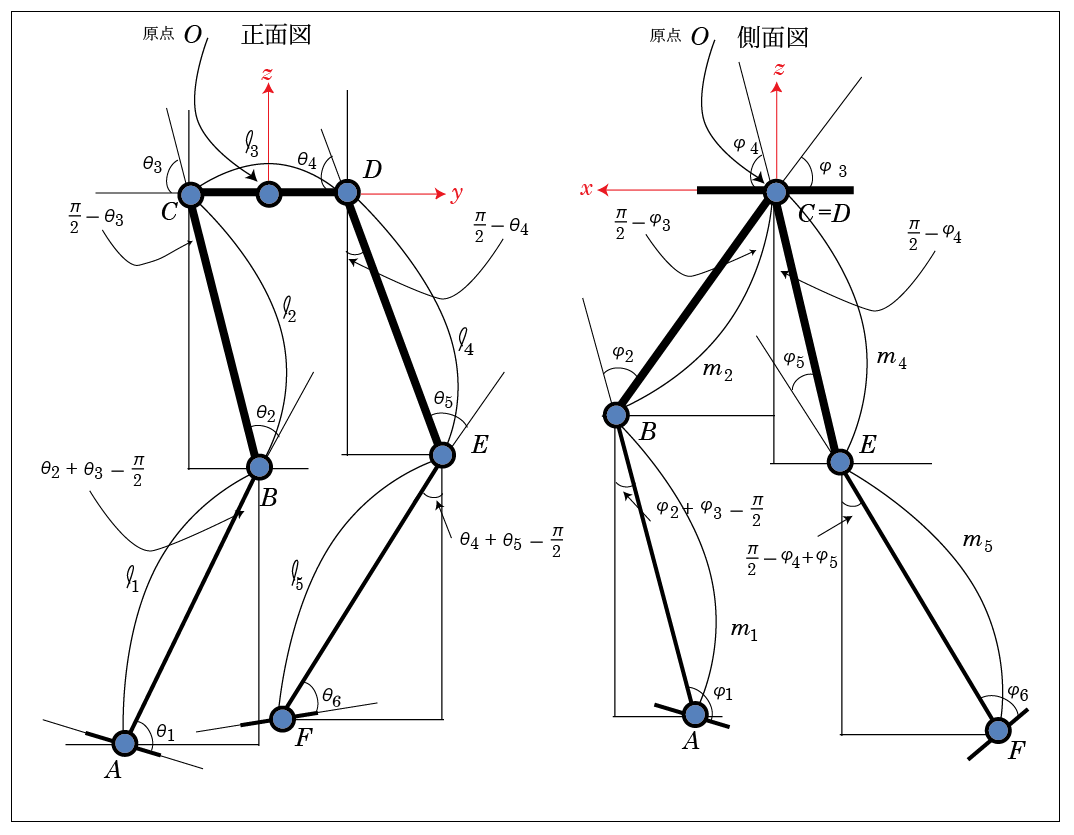
正面図と側面図を同時に書くと上記図のようになる。前回の問題は、ロボットの原点で座標が固定されていなかったことだ。原点の軸においては、回転していなくした。そこで固定して、実際の動きは、それぞれの位置をグローバル座標に変換して表示させるようにすべきだということ。
図はまた、角度の正の向きを定義している。単なる定義であって、定義を変えると途中の式の形は変わるが、結果に変化はない。
原点の座標を として
として の各座標を示そう。ただし、
の各座標を示そう。ただし、 は、座標これらの座標に直接関係せず、ただ、足の向きを規定しているだけなので、ここでは省略する。
は、座標これらの座標に直接関係せず、ただ、足の向きを規定しているだけなので、ここでは省略する。
《正面図》
A点とB点の関係

B点とC点の関係

C点と原点の関係

D点と原点の関係

D点とE点の関係

E点とF点の関係

《側面図》
A点とB点の関係

B点とC点の関係

C点とD点と原点の関係

D点とE点の関係

E点とF点の関係

正面図と側面図の
 軸の座標は一致しなければならないので、式的には
軸の座標は一致しなければならないので、式的には と
と で調整されることになるだろう。
で調整されることになるだろう。つまり、実際の足の長さ、
 と与えられた角度から、
と与えられた角度から、 の全てが計算できるはずだ。次回はそれを考えてみる。
の全てが計算できるはずだ。次回はそれを考えてみる。
足郎2シミュレーターの構成
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_415290769594460e2e485922904f345d.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_415290769594460e2e485922904f345d.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_fbade9e36a3f36d3d676c1b808451dd7.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_fbade9e36a3f36d3d676c1b808451dd7.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_d873aad93c5473fdbf52b2bb0d90d7df.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_d873aad93c5473fdbf52b2bb0d90d7df.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_8508620f1650d75ebbf18f6d590a2d91.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_8508620f1650d75ebbf18f6d590a2d91.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_8493d38b9f3356fba9820236202ec4e4.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_8493d38b9f3356fba9820236202ec4e4.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_868aa005b9230fd181dde581da005b1a.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_868aa005b9230fd181dde581da005b1a.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_1a1b146ff3d40fa704cf722f2d9dd6ef.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_1a1b146ff3d40fa704cf722f2d9dd6ef.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_0cde1496e9da2253948270af829fb632.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_0cde1496e9da2253948270af829fb632.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_5cfd083ed446d37acb33309c4d94b3cf.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_5cfd083ed446d37acb33309c4d94b3cf.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_9dd4e461268c8034f5c8564e155c67a6.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_9dd4e461268c8034f5c8564e155c67a6.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
足郎2のシミュレーター作りが面倒くさい。角度と位置の関係をどのように表すかがわかりにくい。先に書いたものは複雑すぎてわかりにくい。ある論文を参考に、座標を単純にしたことによってグラフィカルに描くことができるようになった。
まず、関節角度をランダムに少しずつ動かした動画は次のようになる(クリックすると再生するはず。マックしかダメか?)。
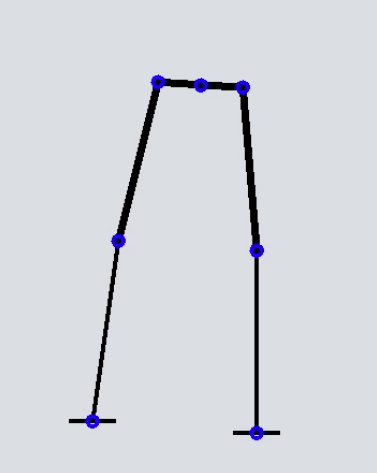
ここまでできれば、サーボモータの動きと連動できる。基本的には、COSM言語で書かれたプログラムをシミュレートできるようにしたい。
まず、理論的な構成を記録しておこう。上記の動きが実現しているのは、以下の理論、数式が基本的に正しかったことを示している。その検証のためのものだ。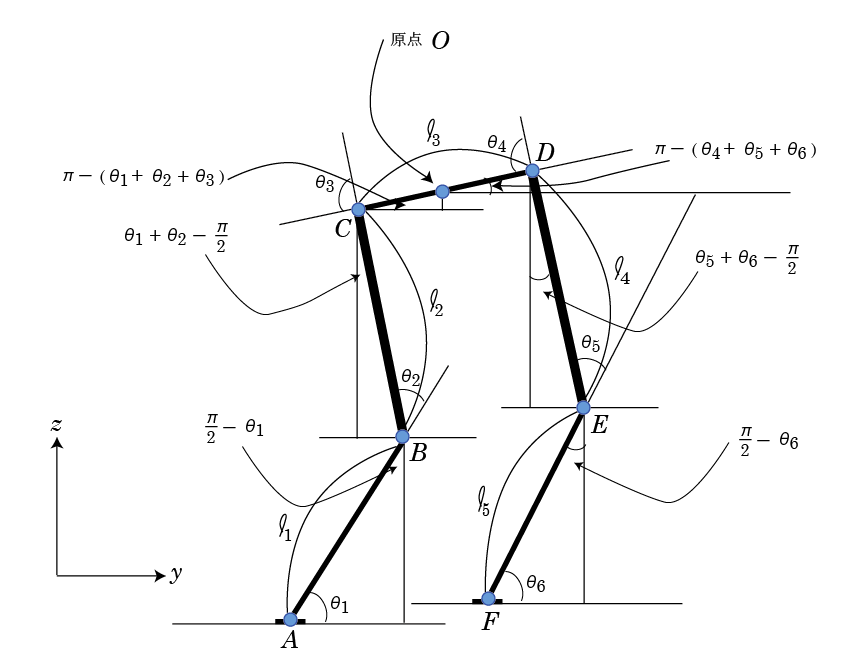
左下に描かれているように、 軸と
軸と 軸のみの表現である。
軸のみの表現である。
複雑そうだが、数学的には極めて単純になる。
図に向かって左側の足
A点とB点の関係:

B点とC点の関係:

C点と原点の関係:

図に向かって右側の足
原点とD点の関係:

D点とE点の関係:

E点とF点の関係:

見ればすぐにわかるように、極めて対称的な関係が求められる。ここで、原点の座標と6つの角度、および各長さが与えられれば、全ての点が決まる。
ただし、六つの角度は全て自由に与えることはできず、

の関係が成立していなければならない。自由度は5なのである。
また、各長さは、実際の長さが、ここでは現れていない
 方向の変位によってきまる。
方向の変位によってきまる。基本的な枠組みはできたので、さらにシミュレーションができるようにする。


