Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_0e22e428b0fc73d336c6d415958da8c9.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_0e22e428b0fc73d336c6d415958da8c9.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_8e81a210a81cf0bf81723a6bf4e47c19.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_8e81a210a81cf0bf81723a6bf4e47c19.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_01bbdf8a17a986d1072d8777784d9e03.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_01bbdf8a17a986d1072d8777784d9e03.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_03e477e98fadb69c91294521ff933b20.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_03e477e98fadb69c91294521ff933b20.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_8a53fb972d1d6e65aef9c876e7b73c41.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_8a53fb972d1d6e65aef9c876e7b73c41.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_eeae567cac1e51de316d11ab0f0a8df1.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_eeae567cac1e51de316d11ab0f0a8df1.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_d3822a506709426c4118368b68711f7f.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_d3822a506709426c4118368b68711f7f.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_1d4f9dc8b15eddee1ebb57bb653f4848.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_1d4f9dc8b15eddee1ebb57bb653f4848.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_0c4ea554c815215628b2c79e48df6405.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_0c4ea554c815215628b2c79e48df6405.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2dfeec3d180f7aa614ebc7b374e25860.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2dfeec3d180f7aa614ebc7b374e25860.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2554a2bb846cffd697389e5dc8912759.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2554a2bb846cffd697389e5dc8912759.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2dfeec3d180f7aa614ebc7b374e25860.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2dfeec3d180f7aa614ebc7b374e25860.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_0c4ea554c815215628b2c79e48df6405.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_0c4ea554c815215628b2c79e48df6405.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_f0ff5cdc8ac1d3d47c40f5439e6d1049.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_f0ff5cdc8ac1d3d47c40f5439e6d1049.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_7694f4a66316e53c8cdd9d9954bd611d.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_7694f4a66316e53c8cdd9d9954bd611d.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_933696ed836a384bbcb65d9689c873b6.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_933696ed836a384bbcb65d9689c873b6.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_14dd5576e3f5892b68f7f35415898069.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_14dd5576e3f5892b68f7f35415898069.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_cd2f66a0ac94c8049d07c9837956362f.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_cd2f66a0ac94c8049d07c9837956362f.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_ca35dc0176826fdc6f41ea91a8d2bea3.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_ca35dc0176826fdc6f41ea91a8d2bea3.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_0c4ea554c815215628b2c79e48df6405.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_0c4ea554c815215628b2c79e48df6405.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_8a4bbd153c74655abb7ca04c0fa901d8.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_8a4bbd153c74655abb7ca04c0fa901d8.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_be63276e664d32b5645ce6071e035c20.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_be63276e664d32b5645ce6071e035c20.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
Warning: fopen(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2dfeec3d180f7aa614ebc7b374e25860.gif): failed to open stream: Permission denied in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 123
Warning: fputs() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 124
Warning: fclose() expects parameter 1 to be resource, bool given in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 126
Warning: getimagesize(/data/htdocs/ibot/wpibot//wp-content/plugins/latex/cache/tex_2dfeec3d180f7aa614ebc7b374e25860.gif): failed to open stream: No such file or directory in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 129
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /data/htdocs/ibot/wpibot/wp-content/plugins/latex/latex.php on line 49
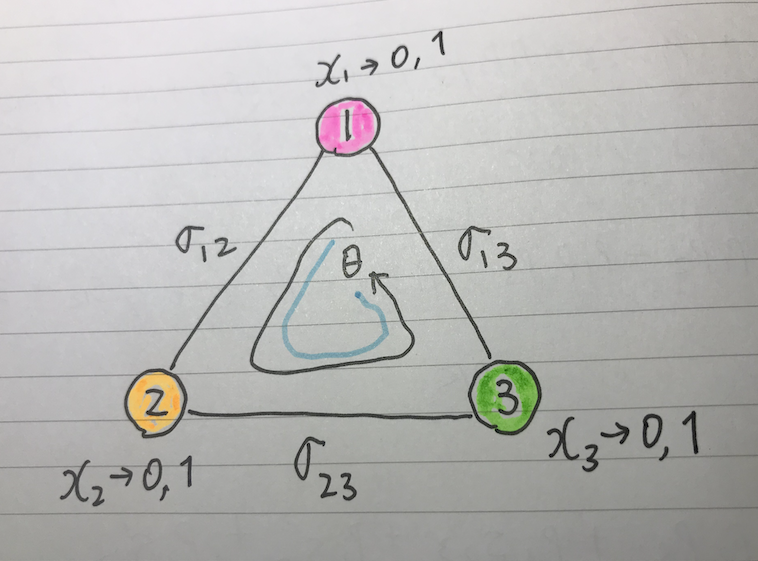
先の記事で導出した3次元の多変量ベルヌーイ分布の同時確率の形を再掲すると、次のようなものである(記号の説明は、前の記事を参照のこと)。








これを一般ベイズ分類器(Naiveではない)の事前確率として利用し、MNISTデータの読み取りをテストすることが次の課題だ。ただ、昨夜布団に入って、ここでの や
や は、事前学習で標本値を作ることができるが、各係数の前についている符号はどのように決定するのかが気になった。そのまま寝てしまったが、今朝、考えたので、それをメモしておく。(図の
は、事前学習で標本値を作ることができるが、各係数の前についている符号はどのように決定するのかが気になった。そのまま寝てしまったが、今朝、考えたので、それをメモしておく。(図の は、
は、 のことである)
のことである)
基本は、正の相関のあるピクセル同士が同じ値を持つ確率は高まる、負の相関の場合は低くなるということである。
そうなると の係数にかかる符号は、次のようにして決まる。まず、それぞれの式の第1の項目は、三つのピクセルの状態と、それらが独立の場合の同時確率を示している。例えば最初の式の場合は
の係数にかかる符号は、次のようにして決まる。まず、それぞれの式の第1の項目は、三つのピクセルの状態と、それらが独立の場合の同時確率を示している。例えば最初の式の場合は で、全てが
で、全てが ということは、すべのピクセルの値が負である状態と言うことである。次に、第二の項は、
ということは、すべのピクセルの値が負である状態と言うことである。次に、第二の項は、 で、その符号は正である。この符号が正である理由は、相関の問題になっている第1ピクセルと第2ピクセルが、ともに0で、同じ方向に動いている、連動しているから、正なのである。その第1式は、全てが連動しているので、すべて正なのである。
で、その符号は正である。この符号が正である理由は、相関の問題になっている第1ピクセルと第2ピクセルが、ともに0で、同じ方向に動いている、連動しているから、正なのである。その第1式は、全てが連動しているので、すべて正なのである。
第2式を見てみよう。その第1項は、 である。ピクセルの状態は、第1,2ピクセルガ0で、第3ピクセルが1となっていることがわかる。第2項は、
である。ピクセルの状態は、第1,2ピクセルガ0で、第3ピクセルが1となっていることがわかる。第2項は、 であるが、この場合も、第1,2ピクセルは連動しているので正である。第3項は
であるが、この場合も、第1,2ピクセルは連動しているので正である。第3項は で、符号は負だが、これは、第1ピクセルが0で、第3ピクセルは1で、方向が逆になっているので、負なのである。
で、符号は負だが、これは、第1ピクセルが0で、第3ピクセルは1で、方向が逆になっているので、負なのである。
ちなみに、 の前についているのが、
の前についているのが、 であるか
であるか であるかは、第1項の組み合わせの中に入っているものがそのまま踏襲されているだけである。
であるかは、第1項の組み合わせの中に入っているものがそのまま踏襲されているだけである。
また は、三つのピクセル値の符号によって決まる。すなわち、その式の第1項のqが含まれていれば(-1)をかけ、pが含まれているならば(1)をかけ、その三つの値の掛け算の符号で決まるのである。つまり、第2式のような場合は、(-1)(-1)(1) だから、正である。
は、三つのピクセル値の符号によって決まる。すなわち、その式の第1項のqが含まれていれば(-1)をかけ、pが含まれているならば(1)をかけ、その三つの値の掛け算の符号で決まるのである。つまり、第2式のような場合は、(-1)(-1)(1) だから、正である。
すなわち、第1項が決まると、式の形は全て決まってしまうと言うことになる。そうすると、3次多変量ベルヌーイ分布の同時確率の一般形もすぐにかけそうだ。それができると、n次多変量ベルヌーイ分布の一般形もかけることになる。ただ、頭の痛くなるほど複雑になるので、今は、書くのをやめておく。